構造物のスケーリング程度を剥離度で示す
剥離度はスケーリングに相当する指標です[8]。実験室ではスケーリング量(単位面積あたりの剥離片の質量)からスケーリングの程度を評価するのが一般的ですが、構造物ではスケーリング量の測定が不可能です。本指針では、構造物のスケーリングの程度を剥離度で示すこととしています。剥離度は、剥離面の上に枠(50cm×50cm)を据え付け、枠内における剥離深さと剥離面積を調べ、下記の式により求めます。
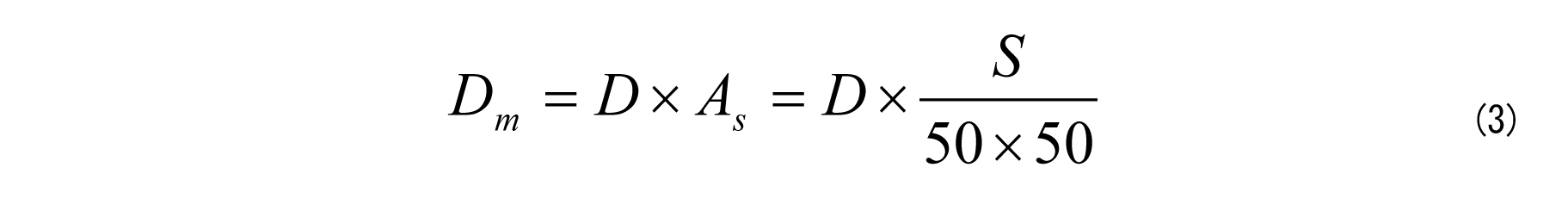
ここに、Dmは剥離度(mm)、Dは剥離深さ(mm)(10点の測定値の平均)、Asは枠内に占めるスケーリング面積の割合、Sは枠内のスケーリング面積(cm2)です。
枠内全面がスケーリングしているときは、剥離深さが剥離度となります。
写真-2 剥離度の測定状況
構造物の凍害ひび割れの程度を相対動弾性係数で示す
相対動弾性係数は、実験室では一次共鳴振動数により評価されます。しかし、供試体の寸法が規定されていること、凍害深さが把握できないことから、この方法を構造物に適用することは厳しいです。そのため、本指針では、凍害が発生している部材からコアを採取し、コアを挟むように超音波の発・受振子をコアの側面にあて、コア内部の超音波伝播速度を深さごとに調べ、超音波伝播速度から各深さの相対動弾性係数を求めることとしています[9]。
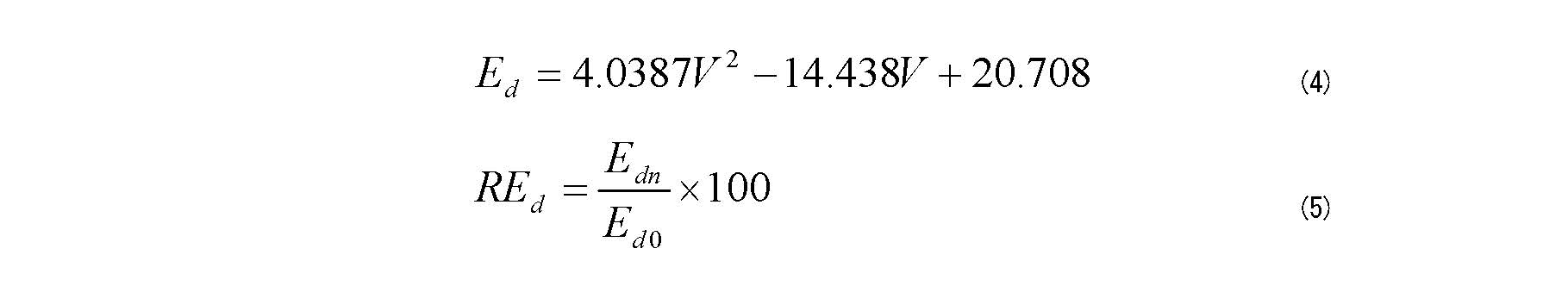
ここに、Edは動弾性係数(GPa)、Vは超音波伝播速度(km/s)、REdは相対動弾性係数(%)、Ednは凍害発生箇所の動弾性係数(GPa)、Ed0は供用開始直後の動弾性係数(値がない場合は、供用中のコンクリート構造物において健全とみなせる箇所の動弾性係数)(GPa)です。
凍害予測の例題
ここで、凍害の予測式の算出例を示します。
例えば、凍害を受けた部材で経年調査(2年に1回、剥離度と深さ5cmの相対動弾性係数を測定)を行い、表-1に示す結果を得たとします。
表-1 調査結果の一例

式(1)、(2)で示した予測式は、図-2のように変形することができます。
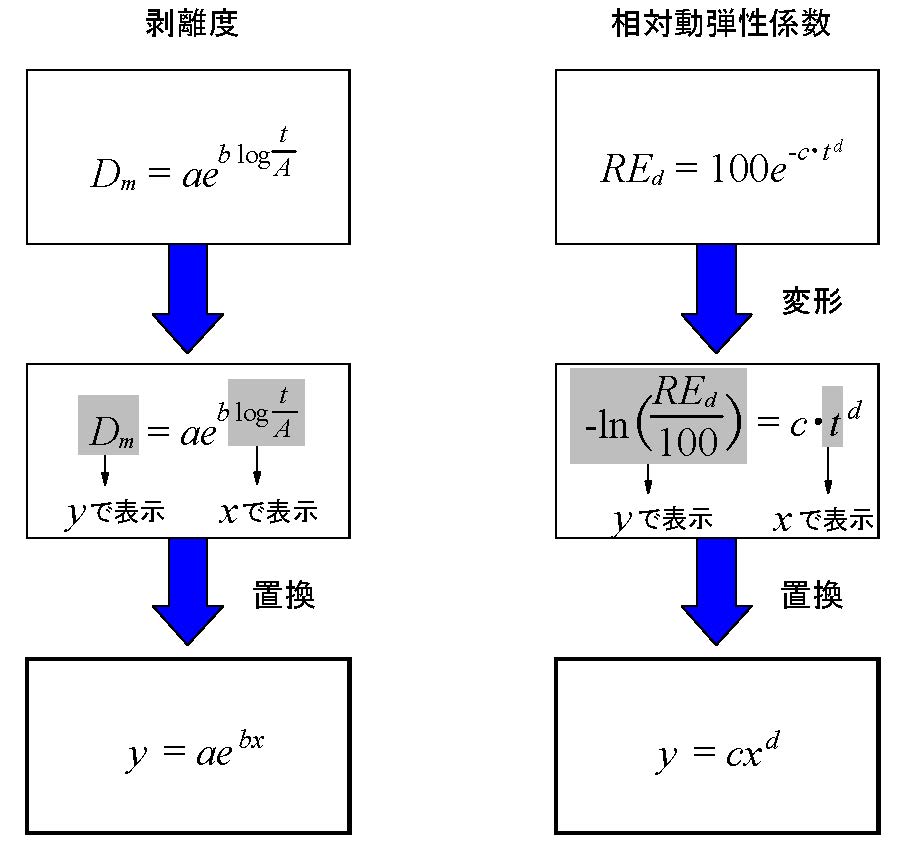
図-2 予測式の変形
図-2で示した変形後の式にならい、予測式の係数(a、b、c、d)を求めます。
はじめに、剥離度について説明します。変形後の式に示されるy、x(図-2の左)は表-2のように整理されます。なお、tを無次元化させるための係数Aは、最長供用年数8年の1/2をとって4としています。
表-2 変形後の式のy、x(剥離度)、なおA=4
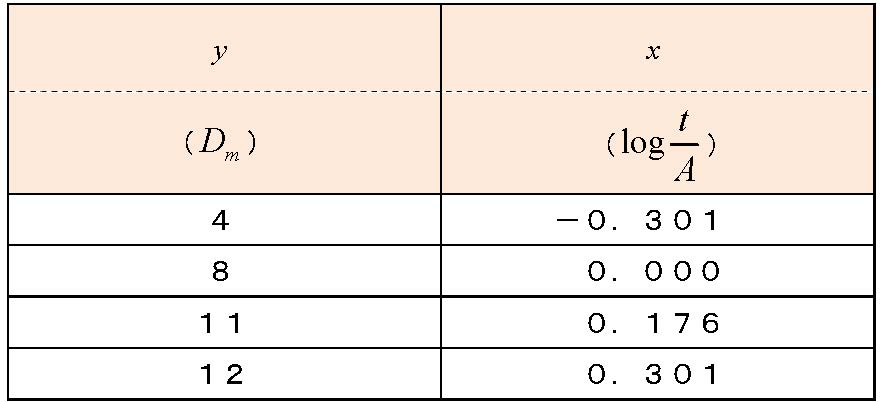
表-2をグラフ化し、Excelの近似曲線機能を活用して指数近似を行うと、図-3に示す回帰式が得られます。この図から剥離度の予測式の係数aは7.42、bは1.88と決定されます。
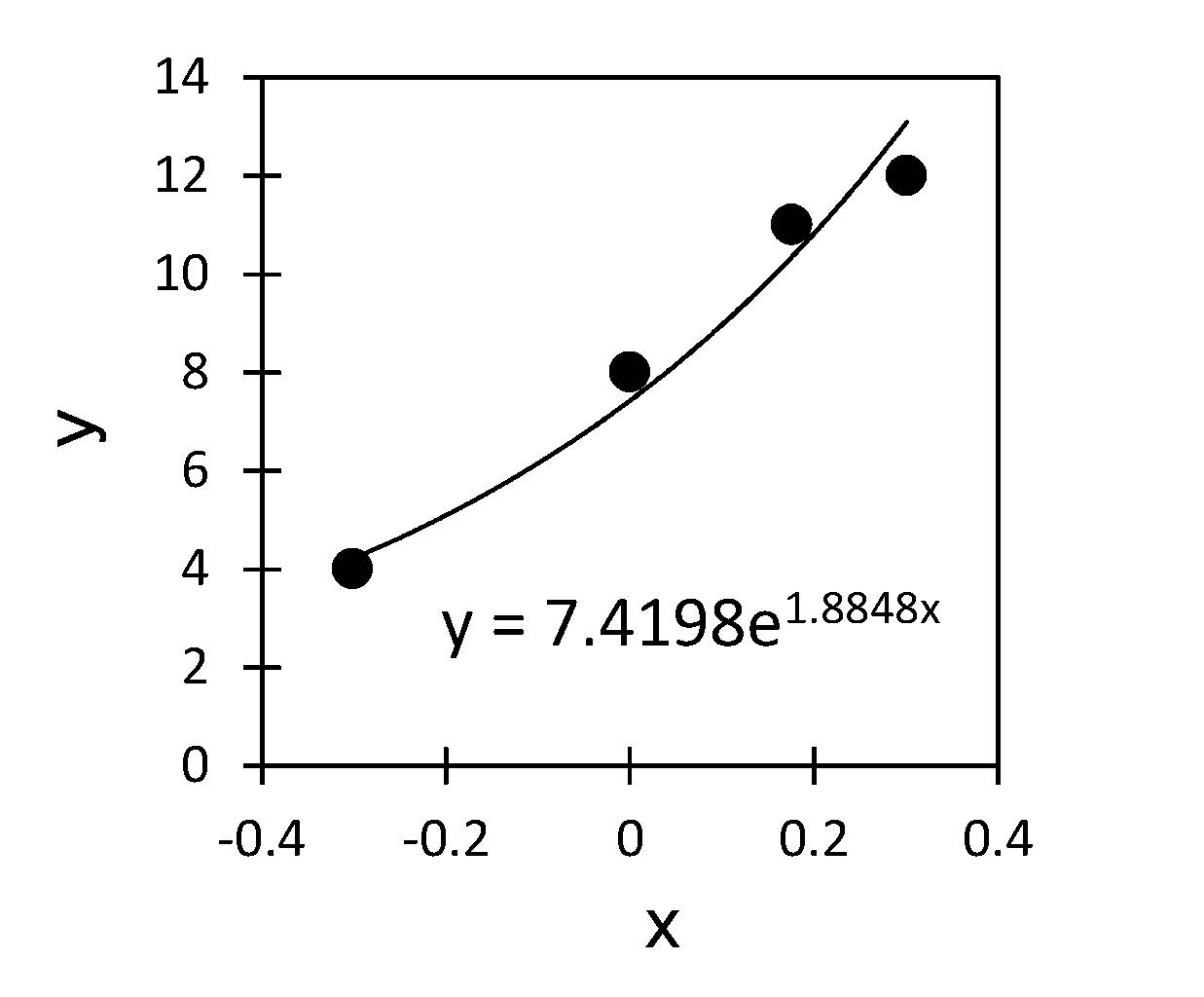
図-3 剥離度の予測式の係数(a、b)の決定
次に、相対動弾性係数について説明します。変形後の式に示されるy、x(図-2の右)は表-3のように整理されます。
表-3 変形後の式のy、x(相対動弾性係数)
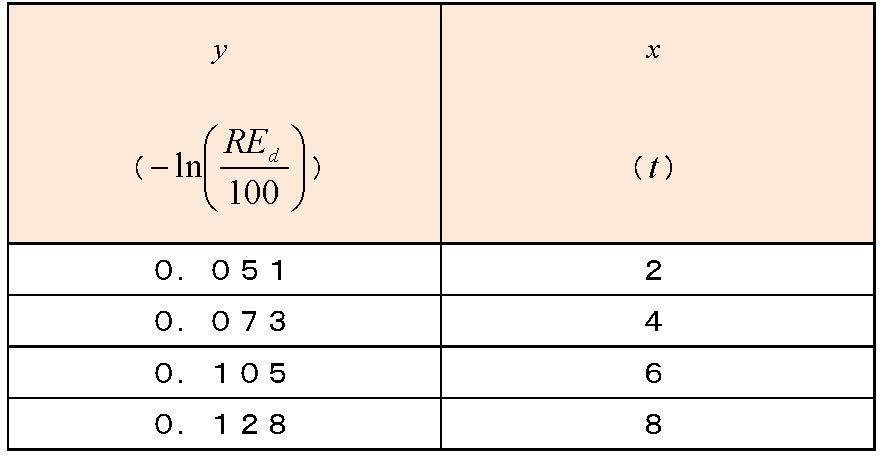
表-3をグラフ化し、Excelの近似曲線機能を活用して累乗近似を行うと、図-4に示す回帰式が得られます。この図から、相対動弾性係数の予測式の係数cは0.03、dは0.67と決定されます。
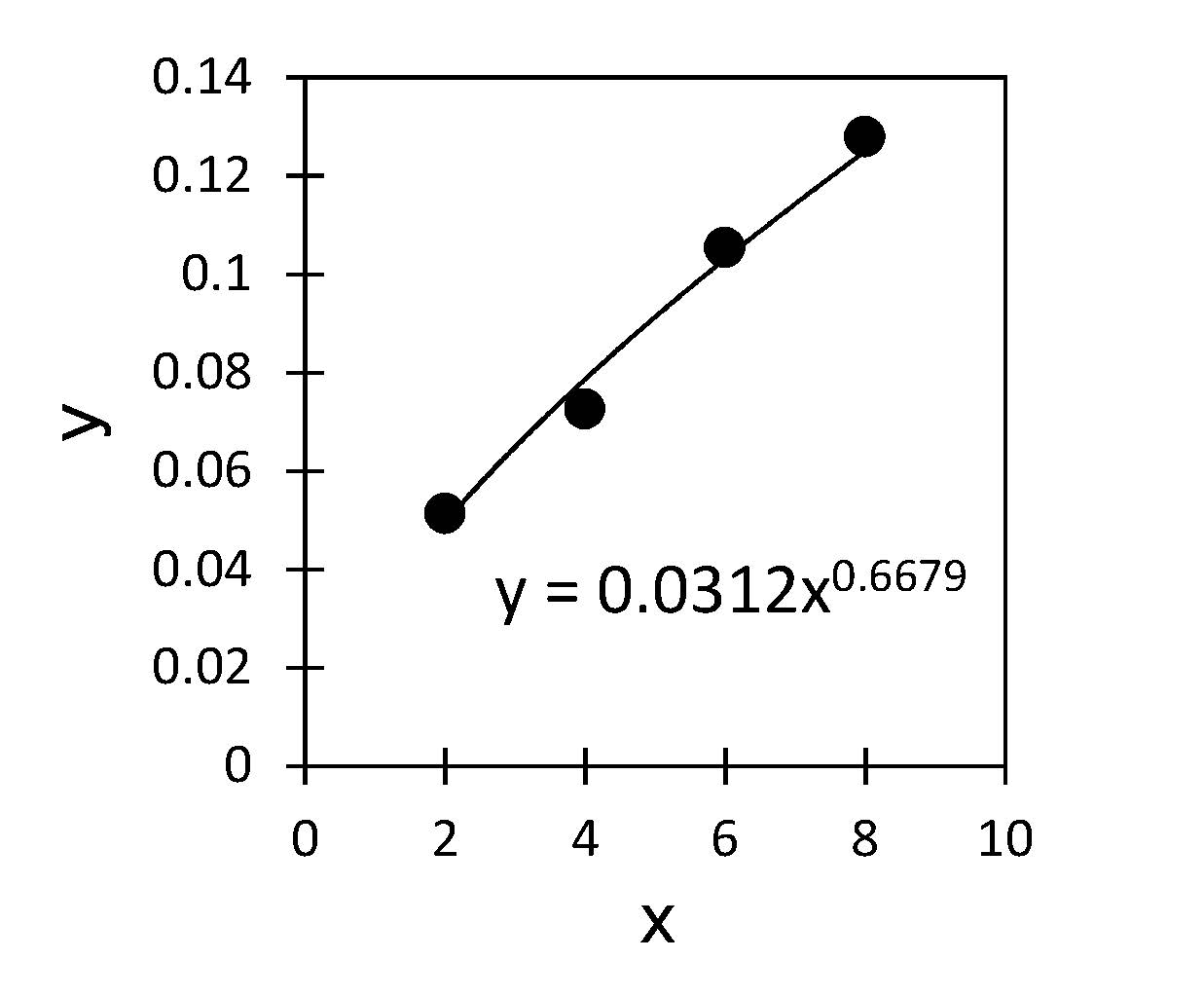
図-4 相対動弾性係数の予測式の係数(c、d)の決定
すなわち、凍害の予測式は次式となり、図-5に示すグラフを得ることができます。
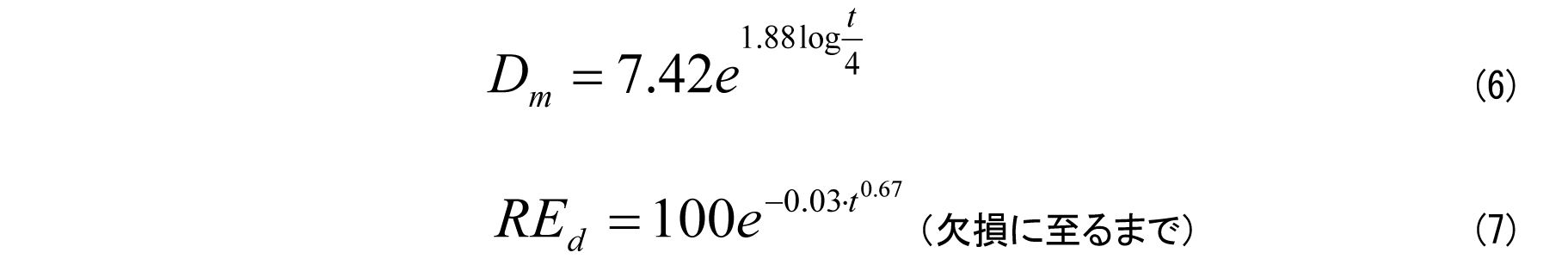
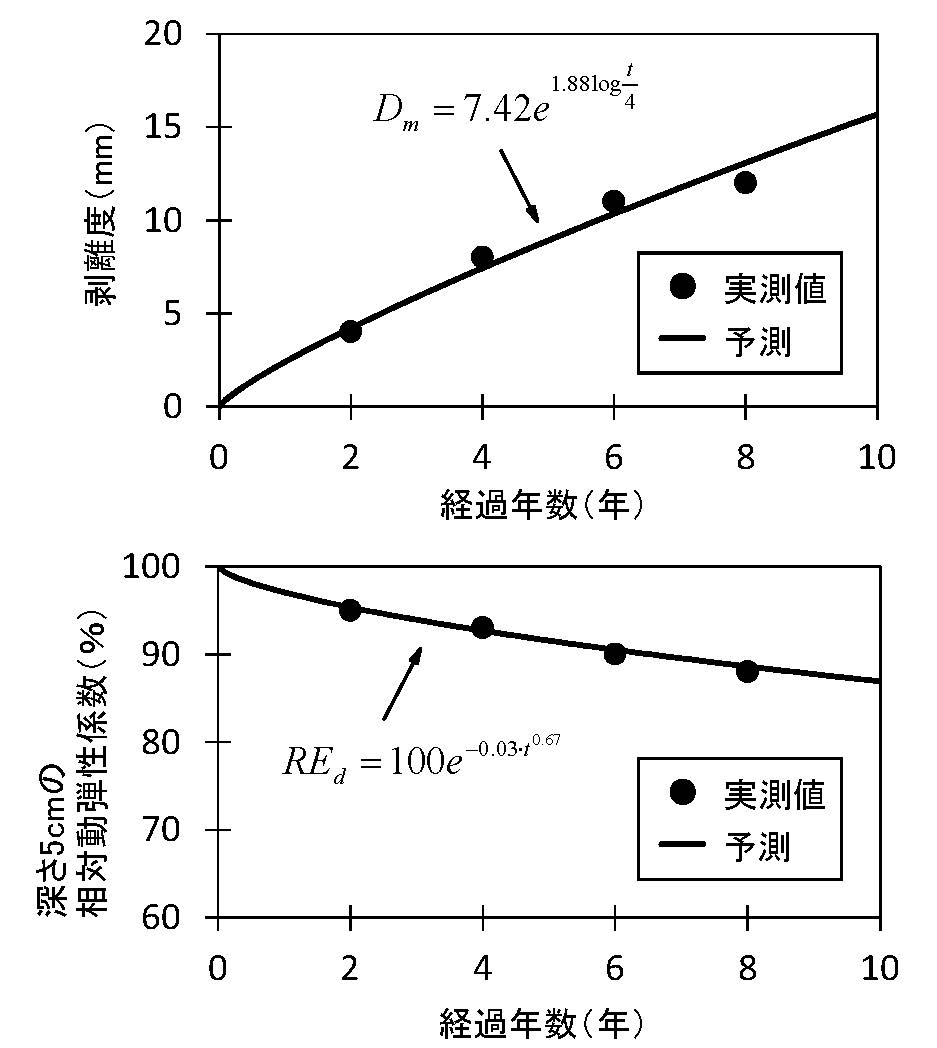
図-5 剥離度および相対動弾性係数の経年変化の予測と実測
なお、この予測式は取得したデータ(表-1)の範囲で求めたものです。そのため、点検データが蓄積されたら、その都度、予測式との整合を確認し、必要に応じて予測式の修正を図ることが望ましいです。






